ICT Gyan

Information and Communication Technology

Standard 10: Practical No 11 a

Practical No 11 a: Verify the theorem: If two circles are touching circles then the common point lies on the line joining their centers.

Circles could either touch Internally or Externally.

Case 1. Circles touching Externally


Only the diagram given in the Output Section should be printed and put in the Journal.

The figures given in the Procedure are only for your understanding.


Aim

To verify the theorem: If two circles are touching externally then the common point lies on the line joining their centers.

Theory

Geogebra has dual representation namely the Geometric View and the Algebraic View. One can construct or modify geometric figures in the geometric section and observe details about the constructed figures in the Algebraic Section. Furthermore constructions can also be performed by typing in the appropriate command in the Input Box.

Tools

  1. Circle with center through point Tool

  2. Segment between two points

  3. Point on Object

  4. Distance or Length

Procedure


1. Open Geogebra. Click on Tool No 5 and select ‘Circle with center through point’.

See Figure 1.


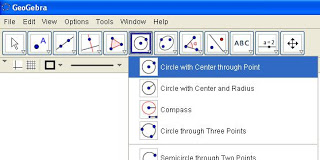
Figure 1

2. Click at any place in the Graphic Area where you want one center ‘A’ of the first circle. Drag your mouse away from the center until you see a circle of appropriate size. Click to get point ‘B’.

See Figure 2.


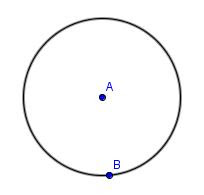
Figure 2

3. Click on any point ‘C’ in the graphic area outside the first circle where you want the center of the second circle.Drag outward until the two circles are just touching. Click to get point ‘D’.

See Figure 3.

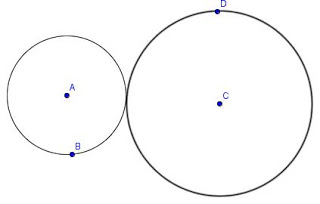
Figure 3


4. Click on Tool No 2 and select ‘Segment between two points’.

See Figure 4.


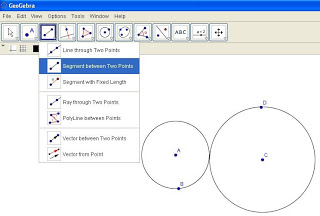
Figure 4

5. Click on ‘A’ followed by ’C’.

See Figure 5.



Figure 5

6. Click on Tool 1 and select ‘Point on Object’

See Figure 6


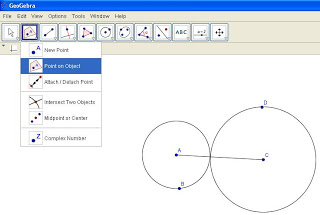
Figure 6

7. Click anywhere on Segment AC. A New Point ‘E’ will appear where you have clicked.

See Figure 7.

8. Drag the point ‘E’ till it lies on the point where the two circles touch each other.


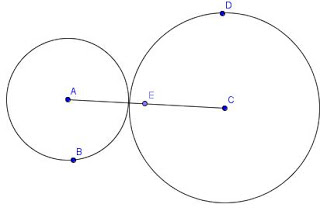
Figure 7

9. Click on Tool 7 and select ‘Distance or Length’ Tool.

See Figure 8.



Figure 8

10. Click on Point ‘A’ followed by point ‘E’. Click on Point ‘E’ followed by point ‘C’. Click on Point ‘A’ followed by point ‘C’.

See Figure 9.

11. In the Algebra Section verify that length(AC) = length(AE) + length(EC). This proves that A-E-C, i.e., the point of contact of two touching circles lies on the line joining their centers.


Figure 9

Output


Final Figure

Conclusion

Thus we have verified the theorem: If two circles are touching externally then the common point lies on the line joining their centers.