ICT Gyan

Information and Communication Technology

Standard 10: Practical No 10

Practical No 10: Verify the theorem: The measure of an angle subtended by an arc at a point on the circle is half the measure of the angle subtended by the same arc at the center.


Only the diagram given in the Output Section should be printed and put in the Journal.

The figures given in the Procedure are only for your understanding.


Aim

To verify the theorem: The measure of an angle subtended by an arc at a point on the circle is half the measure of the angle subtended by the same arc at the center.

Theory

Geogebra has dual representation namely the Geometric View and the Algebraic View. One can construct or modify geometric figures in the geometric section and observe details about the constructed figures in the Algebraic Section. Furthermore constructions can also be performed by typing in the appropriate command in the Input Box.

Tools

  1. Circle with center through point Tool

  2. New Point Tool

  3. Segment between two points Tool

  4. Angle Tool

Procedure


1.Open Geogebra. Select Tool No 5 and click on ‘Circle with center through point’.

See Figure 1.


Figure 1

2. Click on any point ‘A’ where you wish the center of the circle to be. Move your mouse away from the center and you will observe a circle. Click (point ‘B’) when you have a circle of appropriate size.

See Figure 2.


Figure 2

3. Click on Tool 1 and select the ‘New Point Tool’.

See Figure 3.





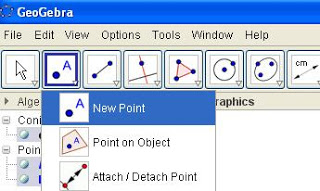
Figure 3




4. Click on two points ‘C’ and ‘D’ on the circle as shown.

See Figure 4.


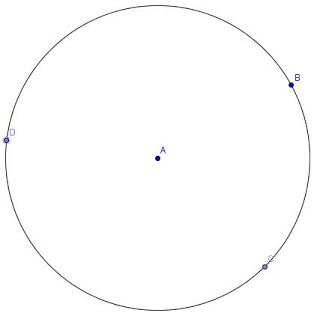
Figure 4

5. Click on Tool 2 and select ‘Segment between two points’ tool.

See Figure 5.



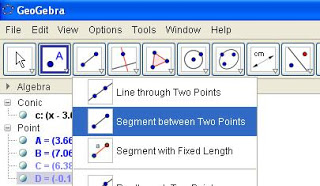
Figure 5

6. 6. Click on Point ‘A’ followed by ‘B’.

7. Click on Point ‘A’ followed by ‘C’.

8. Click on Point ‘D’ followed by ‘B’.

9. Click on Point ‘D’ followed by ‘C’.

The result should now look like Figure 6


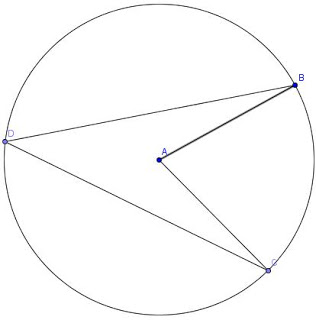
Figure 6

10. Click on Tool 7 and select the ‘Angle’ tool.

See Figure 7.

11. Click on Points ‘C’, ‘A’ and ‘B’ one after the other. The angle CAB will be marked out.

12. Click on Points ‘C’, ‘D’ and ‘B’ one after the other. The angle CDB will be marked out.


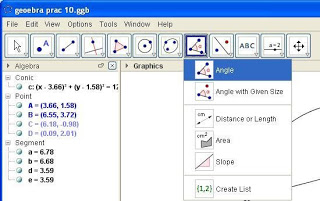
Figure 7

13. In the Algebra Section, the Angles CAB and CDB will be indicated as ‘α’ and ‘β’ respectively.

Verify that α = 2xβ

14. Save or print your file if required.

See Figure 8.



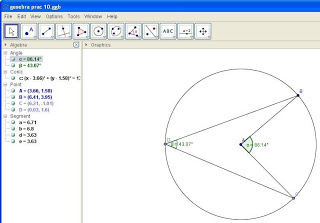
Figure 8

Output


Final Figure

Conclusion

Thus we have found the mean, median and mode of the given data.